Игрок взаимодействует с любой компьютерной игрой с помощью ее экрана. Неважно, какой у Вас монитор — плоский ЖК или выпуклый ЭЛТ, экран игры всегда есть плоскость. В играх Х3 помимо моделей кораблей, станций, астероидов и т.д., находящихся как бы за плоскостью этого экрана, есть элементы игрового интерфейса, такие как различные меню, которые находятся непосредственно на экране. К ним относятся и элементы HUD (Head-up display), призванные информировать игрока при пилотировании. Некоторые из этих элементов меняют свой вид в зависимости от того, какой тип управления полетом корабля Вы используете.

   Управление мышью.

     1.   2.

1. Всегда расположен строго в центре экрана, служит прицелом для стрельбы с помощью клавиатуры (по умолчанию клавиша Ctrl).
2. Курсор, свободно перемещается по экрану, служит указателем направления, а также прицелом для стрельбы с помощью мыши (по умолчанию ПКМ).

   Управление клавиатурой.

     3.   4.

3. Всегда расположен строго в центре экрана, служит прицелом для стрельбы с помощью клавиатуры (по умолчанию клавиша Ctrl).
4. Курсор, свободно перемещается по экрану, при нажатой ЛКМ служит указателем направления, а также прицелом для стрельбы с помощью мыши (по умолчанию ПКМ).

     5.  

5. Этот элемент служит точкой упреждения для стрельбы по цели как с помощью мыши, так и с помощью клавиатуры, на его перемещение в плоскости экрана оказывает влияние сумма факторов. Принадлежит только цели, является центром окружности, в которой возможен "захват цели" при включенном режиме автоприцела.

   В виртуальном космосе игры любой трехмерный объект, который можно выделить целью, включая и корабль игрока, обладает линейными размерами и осями вращения. Пересечения этих осей образуют точку Х, являющуюся, по сути, шаровым шарниром с тремя степенями свободы. Каждый объект, выделяемый целью, имеет также свою рамку, изображаемую на игровом экране и имитирующую собой плоскость Х, проходящую через точку Х объекта. Эта плоскость Х всегда параллельна плоскости игрового экрана. Точка Х и плоскость Х являются важными элементами объекта (рис.1).

      
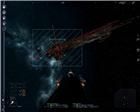
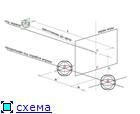      рис.1                             рис.2   
 
   На рисунке 2 изображена изометрическая схема, разъясняющая, каким образом игровой экран связан с трехмерными объектами в игре, где:
   Х — точка центра вращения модели цели,
   W — точка центра вращения модели пилотируемого игроком корабля,
   V — точка обзора, находится строго в центре игрового экрана, имитирует обзор из кокпита истребителя или с мостика корабля.
   Видно, что ни точка Р (низ экрана), ни точка V не являются центрами вращения судна игрока, а следовательно, и всего пространства вокруг. Расстояние от точки обзора до точки вращения характеризуется величинами w и h. Для каждого корабля они различны, w может иметь отрицательное значение. Например, для Пантеры w = 0 (рис. 3), а для Деймоса h = 0, то есть для пилота Деймоса продольная ось вращения совпадает с осью вращения игрового экрана (рис. 4). Для большинства же истребителей характерна схема, когда точка W находится ниже и чуть спереди точки обзора V (рис. 5). Если, положим, Вы совместите ось экрана с точкой упреждения для неподвижной цели в качестве ориентира и начнете вращаться с помощью клавиши Q или E, то вращение будет происходить с некоторым эксцентриситетом к оси экрана. Этот эксцентриситет и есть величина h.

        
      рис. 3                            рис. 4                            рис.5

   Станции в игре, которые, между прочим, тоже можно двигать, могут иметь несколько точек Х, по одной на каждый стыковочный узел. И хотя станции в космосе не вращаются вокруг своих узлов, вращаются их плоскости Х относительно плоскости экрана игрока, всегда соблюдая обоюдную параллельность.  Расстояние от точки V (не от W) именно до точки Х отображается, как расстояние до цели, хотя "расстояние" до модели объекта всегда меньше этой величины, потому что модель объемна и может иметь весьма нескромные размеры. Так же и расстояния от одного города до другого в дорожных атласах указывается не от/до городских границ, а от/до координат административного центра населенного пункта или так называемого "нулевого километра". Эта точка, например, в Москве находится рядом с Красной площадью.  В случае со станциями, у которых не один стыковочный узел, расстояние указывается до ближайшего, он же и отображается целью.
  


   Игровая баллистика, описываемая здесь, имеет мало общего с баллистикой, как наукой или комплексом физико-технических дисциплин, охватывающих теоретическое и экспериментальное исследование движения метаемых твердых тел — пуль, артиллерийских снарядов и т.д. Потому, что в нашем случае все это:
   во-вторых, происходит в космосе;
   и во-первых, — в компьютерной игре.
Здесь выложены приобретенные данные о так называемой "внешней баллистике" игры, занимающейся движением снарядов в пространстве между пусковой установкой и целью. Баллистика самих космических летательных аппаратов не рассматривается.
   Целью является выявление некоторых особенностей в игровой механике. Здесь мне приходится употреблять придуманные и названные мной термины.

  Траектория полета снаряда — линия движения выпущенного из ствола лазера светового пятна, видимого на экране игры и символизирующего снаряд.
  Кучность оружия — свойство оружия испускать снаряды близко к траектории.
  Гибкость оружия — способность оружия испускать снаряды не вдоль оси своего неподвижного ствола, а с некоторым углом к ней.
  Угол захвата цели — угол между осью ствола и условной линией наведения на цель, при котором возникает возможность захватить цель и поражать ее автоматически, то есть не целясь. О том, что такое автоприцеливание и как оно работает, можно прочесть здесь.
   Траектория может не совпадать с осью ствола орудия, из которого выпущен снаряд. Это особенность визуализации выстрелов в игре. Траектория всегда прямолинейна. После того, как снаряд выпущен из ствола, он не может изменить свою траекторию. Выпущенный снаряд будет лететь по своей траектории, не меняя скорости полета до тех пор, пока не встретится с препятствием или не исчерпает длину дальности стрельбы данного вооружения, при этом сохраняя свои характеристики урона на всем протяжении полета. После преодоления снарядом своего рубежа дальности, он... исчезает. Дальность полета снаряда, скорость полета снаряда и повреждения по щиту и корпусу цели для конкретного вида вооружения приведены в Характеристиках оружия.
   Для окончательного осознания прямолинейности траектории испускания выстрелов в игре, предлагаю взглянуть на рисунки 6 и 7:

        
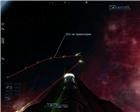
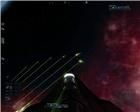
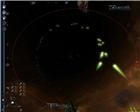
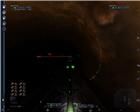      рис. 6                            рис. 7                            рис. 8                            рис. 9

   Пусть Вас не смущают зеленые хвостики от светящихся пятен самих снарядов, которые направлены совсем не по оси истинных траекторий, а совсем наоборот, скорее вдоль ложной. Этот визуальный эффект получается оттого, что снаряд в игре — это не только светящаяся точка, но и принадлежащий ей "хвост", вылет которого из ствола пушки тоже занимает какое-то время. В результате, если производить выстрелы с неподвижного корабля, "хвосты" направлены вдоль истинной траектории, если при этом придать кораблю вращение вокруг его вертикальной оси, то "хвосты" начнут "отклоняться", и чем выше угловая скорость вращения, тем сильнее. А если это делать на движущемся на большой поступательной скорости и вращающемся в горизонтальной плоскости корабле, то получим эффект, представленный на рисунках. К слову, вращаться можно как угодно, не только в горизонтальной плоскости. Ваши выстрелы из Плазменной пушки будут напоминать мазки кистью в зеленой краске по холсту игрового экрана, лентой бегущего из-под Вашего звездолета.
   Орудия главных слотов всех представленных в игре кораблей обладают гибкостью, характеризуемой углом отклонения траектории полета снаряда от оси ствола. Для того, чтобы лучше понять, что такое гибкость оружия, надо на неподвижном корабле произвести выстрелы с помощью ПКМ по произвольной окружности, заведомо отклонив курсор подальше от центра экрана (рис. 8). Выстрелы "нарисуют" некую окружность О₁, за пределы которой не отправится ни один снаряд. Эта окружность имеет определенный радиус R₁ (рис. 9), одинаковый для всех кораблей, независимо от класса корабля и используемого вооружения в главных слотах, при условии, что не меняется разрешение экрана и не используется монитор с другой диагональю. Так же этот радиус не зависит от того, сколько используется лазеров и как именно они расположены на корабле, пусть даже они все будут на одном "крыле". Только ширина дуги этой окружности может немного варьировать во временном отрезке, что обусловлено кучностью стрельбы. Центр этой окружности всегда совпадает с центром игрового экрана.
 
      
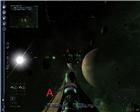
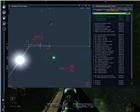      рис. 10                           рис. 11                           рис. 12

   Существует ли практическая польза от знания радиуса этой окружности, не отображаемой на экране? Небольшая, но существует. Например, это позволяет оценивать начало атаки и экономить боеприпасы к огнестрельному и энергию к энергетическому вооружению.
   Но так как пилоты используют разные мониторы с разными линейными характеристиками, то имеет смысл применять не радиус этой окружности, а угол отклонения траектории. Если игрок активно использует автоприцеливание, то применим еще так называемый "угол захвата цели", который характеризует область экрана, где возможен этот захват. На рис. 10 эта область описана окружностью О₃. Точнее, окружностями, выбирайте любую.
   Совершенно не важно, вводить ли ось экрана в правую (рис. 10) окружность О₃ или площадью центрального кружка О₃ ловить точку упреждения. Результат будет одинаков — цель будет захватываться. При условиях, конечно, что на корабле игрока установлен хотя бы один из Боевых программных модулей и автоприцел включен.
   На рис. 10 графически представлены площади игрового экрана, где стрельба главной батареей может быть актуальной, если пилот "летает" клавиатурой, а стреляет мышью — окружность О₁ и где цель может поражаться автоматически, если пилот вне зависимости от способа "летания" стреляет клавиатурой — окружность О₃.

   Можно попытаться высчитать эти углы отклонения и захвата. Так как оси стволов параллельны оси экрана и их количество и расположение не влияют на эти углы, то можно для вычисления углов использовать ось экрана. 
   Вычислим угол захвата. Для этого создадим прямоугольный треугольник с вершинами А, В, С (рис. 12) с помощью истребителей в качестве целей. Цель С нужно перемещать по линии, перпендикулярной оси корабля-наблюдателя А, направленной на цель В, до тех пор, пока цель С не станет захватываться автоприцелом корабля А (рис. 11). Расстояния от А до целей В и С известны. Вычисляем cos у:

В моем случае АВ = 1.96 км, АС = 1.98 км ;        cos у = 1.96/1.98 = 0.98 (98 в периоде) ~ 0.99

   Посмотрев в Таблицы Брадиса или подставив значение 0.99 в формулу отсюда, получим arccos 0.99 = 8.10961446°.
Аналогичным образом вычисляем угол отклонения а. Полученные величины для удобства округлим :

                                                                                                           значение угла у : угол захвата = 8°.
                                                                                                           значение угла а : угол отклонения = 31°.

   Если померить угол у по рис. 12 транспортиром, то получим значение 5°. Чтобы при первом способе вычисления угол у равнялся 5°, надо, чтобы расстояние АВ увеличилось всего примерно на 12 метров, то есть на ~1/160 своей длины. Это говорит о том, что в обоих методах неизбежны погрешности: расстояния грубо округлены, угол АВС оказался не прямым, а плоскость треугольника ABC лежит не параллельно плоскости эклиптики. То есть, значения вычисленных углов приближенные.

      
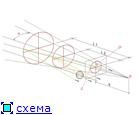
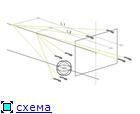      рис. 13                           рис. 14                           рис. 15

   На рис. 13 и 14 схематично изображены углы захвата у и отклонения а. Они приложены к некой точке Q, которая олицетворяет собой игрока перед монитором компьютера. Окружности в плоскости экрана нужны для того, чтобы имитировать присутствие игрока в виртуальной реальности "заэкранья". Реальное расстояние q от игрока до плоскости экрана никак не влияет на углы в игре.
   На рис. 14 точка С — это курсор мыши, при помощи которой ведется стрельба по пустому пространству с максимальным (для этих условий) углом отклонения, L1 и L2 — дальность стрельбы для, соответственно, лазеров 1 и 2. Для наблюдателя Q траектории лазеров с различной дальностью фокусируются в одной точке С. На рис. 15 стрельба ведется клавиатурой. Расположение лазеров не важно, они могут принадлежать как одной, так и разным группам.

   При стрельбе выпущенные из разных стволов снаряды фокусируются в некоторой точке пространства.
 
        
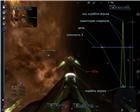
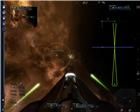
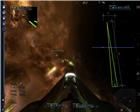
      рис. 16                          рис. 17                           рис. 18                           рис. 19

   Если направление на цель и линия оси экрана составляют значительный угол, то снаряды, выпущенные по курсу при помощи клавиши на клавиатуре (по умолчанию Ctrl), фокусируются в точке, расстояние b до которой равно дальности стрельбы для данного лазера (рис. 16). Сокращая этот угол, можно достичь значения, при котором траектории выстрелов станут перекрещиваться, фокусируясь на плоскости Х (рис. 17). Так происходит только если пилот управляет своим кораблем при помощи клавиатуры. При этом угол до цели будет почти вдвое превышать угол захвата. Таким образом выявляется некая окружность с радиусом n.
   Если, сохраняя этот радиус и управление клавиатурой, выстрелить по площади этой окружности с помощью ПКМ, то траектории выстрелов опять будут фокусироваться на расстоянии b (рис. 18). И только если при таких условиях стрелять в границы Рамки объекта, траектории начнут фокусироваться на плоскости Х (рис. 19).
   Рамки объектов, живущие в плоскости игрового экрана, тоже являются элементами HUD. Они меняют свой размер от минимального до максимального значений в зависимости от расстояния до объекта. На рисунках выше определяются площади в плоскости Х, на которые приходится фокусировка лазеров при стрельбе:
   клавиатурой — окружность с радиусом n,
   мышью — границы Рамки объекта.
   Приближаясь к цели, можно достигнуть расстояния, когда Рамка объекта перестанет увеличиваться. И далее можно отметить изменения границ площади фокусировки для стрельбы мышью. Для клавиатуры окружность О₂ (рис. 20) не меняется.
   Следующие рисунки - это коллажи из нескольких скриншотов каждый.

        
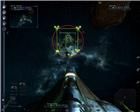
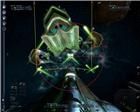      рис. 20                           рис. 21                           рис. 22                           рис. 23

   На этих рисунках  можно заметить увеличение области фокусировки (отмечено желтым маркером) для стрельбы мышью; область меняется в зависимости от взаимного расположения кораблей. Здесь объект выбран целью, чтобы указывалось расстояние до него, но фокусировка на плоскость Х объекта происходит и без указания его целью. Также видно, что точки фокуса не выходят за окружность О₁. Заштрихованная область АВС (рис. 23) является областью плоскости Х, на которую возможно фокусирование.
   К плоскостям Х малых объектов проще приблизиться.

      
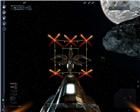
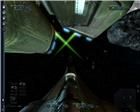      рис. 24                           рис. 25                           рис. 26

   Видно, как область фокусировки искажается при приближении к объекту (рис. 24 и 25). На рис. 25 голубым кружком отмечен несфокусированный выстрел. А точка N показывает сфокусированный выстрел, фокус которого находится вне заштрихованной области, потому что плоскость Х не ограничивается никакими линиями. Но если выстрелить курсором по точке N, выстрел не сфокусируется.
   Надо не забывать, что расстояние в 6 метров указано от точки V (центр на экране) до точки Х вращения цели, а не до плоскости Х. Поэтому и более крупный истребитель способен фокусировать выстрелы на ту же площадь при тех же условиях (рис. 26).
   Все это также верно и для крупных кораблей. Вы сможете попасть из Ударно-импульсных генераторов по М5, мельтешащему перед носом Вашего Деймоса, так как орудия будут фокусироваться на плоскость Х Вашей цели.

        
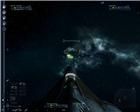
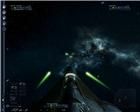
      рис. 27                           рис. 28                           рис. 29                           рис. 30

   На рис. 27 схематично изображена область фокусирования траекторий выстрелов на плоскости Х для клавиатуры в виде окружности О₂. Но с этой областью не все так однозначно, как с окружностью О₃.
   Если совершать маятниковые маневры боковым стрейфом перед целью, поливая ее огнем, то можно обнаружить, что фокусировка начинается, когда ось экрана минует точку Х, и заканчивается, когда расстояние до точки Х в плоскости Х превышает радиус R₂ (рис. 22). Это не связано ни с искажением окружности О₂, ни с запаздыванием фокусировки. Это говорит о том, что радиус R₂ окружности О₂ нужно прикладывать к точке V, а не к проекции точки Х объекта на плоскость экрана, как это неправильно показано на рис. 27. А на рис. 28 и 29 представлен визуальный эффект, связанный с относительно малой скоростью полета снаряда данного лазера. Если то же самое повторить с использованием Импульсного лазера, то эффект пропадает.

   Итак, для пилота, "стреляющего" клавиатурой, в игре есть ориентиры в виде трех окружностей (рис. 30), каждую из которых можно грубо описать так:

• Большая — куда вообще можно выстрелить
  
• Средняя — где цель будет в фокусе Ваших орудий
  
• Малая — где цель будет поражаться автоматически

Большой окружностью нужно захватывать модель или часть модели неприятельского корабля

Средней окружностью нужно захватывать центр Рамки объекта неприятельского корабля

Малой окружностью нужно захватывать точку упреждения для неприятельского корабля

   Все написанное для ведения огня главной батареей справедливо, если игрок самостоятельно ведет огонь с какой-нибудь турели.

   И что же, выстрелы всегда будут попадать только в область окружности О₁ и не смогут выходить за ее пределы?
   Смогут.
   А захваченная цель всегда поражается огнем с клавиатуры?
   Нет, не всегда.

        
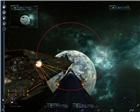
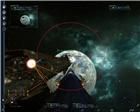
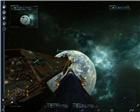
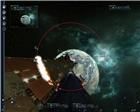
      рис. 31                           рис. 32                           рис. 33                           рис. 34

   До сих пор я применял угол отклонения траектории полета снарядов для описания гибкости оружия. Даже "вычислил" его для стрельбы мышью по пустому пространству. Но этот угол не является максимальным. Например, на рис. 25 видно, как сильно отклонены траектории снарядов, сфокусированные на точку N. Причина в чрезмерной близости плоскости Х от плоскости экрана. Что еще может повлиять на такое сильное искажение угла отклонения а (рис. 14)?
   На рис. 31 видно, что снаряды, выпущенные мышью, фокусируют пятно контакта с моделью цели, не выходя за пределы окружности О₁. На рис. 32 показано ведение автоматической стрельбы по захваченной цели группой лазеров из того же положения относительно цели. Пятно контакта выходит за окружность О₁. При этом, лазер № 8 уже исчерпал лимит своего действительно максимального угла отклонения. Если приблизиться к точке Х еще всего на один десяток метров (рис. 33), остальные лазеры тоже "устают гнуться". На рис. 34 точка С определяет угол отклонения а , а точки по дуге окружности между точками А и В определяют углы, сильно превышающие угол отклонения а.
   При захваченной цели стрельба автоматом ведется с фокусом по точке Х. Все, что находится на линии огня, поражается.
   У некоторых моделей крупных кораблей есть особенности. Они, как цели, обладают не только одной точкой фокусировки траекторий огня. Эти лишние точки находятся на кончиках моделей турелей.

        
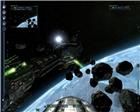
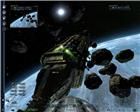
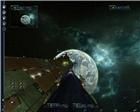
      рис. 35                           рис. 36                           рис. 37                           рис. 38

   На рис. 35 автоприцел фокусирует огонь на пересечении плоскости Х с осью экрана и на кончике ближайшей к нам модели турели. Наличие самой установленной модели турели на корабле-цели не требуется. На рис. 36 огонь ведется по тому месту, где должен располагаться кончик отсутствующей турели. То есть, эти точки фокусировки принадлежат самой модели корабля. Но не все турели могут указывать наличие этих точек.
   На рис. 37 огонь фокусируется на точке Х, так как модель корабля-цели не обладает дополнительными точками для фокусировки автоприцелом. А на рис. 38 фокусировка идет и на точку Х, и на пересечение плоскости Х с осью экрана, хотя у этого корабля есть дополнительные фокус-точки. Здесь получается, что захваченная цель не поражается одним из лазеров, как и в случае с лазером № 8 на рис. 32. А на рис. 33 по захваченной цели мажет вся группа.

   Радиусы окружностей О₁, О₂ и О₃ в X3:Albion Prelude изменились по сравнению с X3:Terran Conflict, так как изменились углы отклонения а, фокусировки b и захвата у. Теперь они увеличены, то есть попадать по мишеням в новом аддоне стало легче.
   Можно сравнить эти окружности для Х3:ТС версии 3.2 и Х3:АР версии 1.1, которые для наглядности представлены на рис. 39:

  
      рис. 39